BackclockingA5/1 Basics in a little more detail¶
The A5/1 cipher is a combination of 3 LFSRs (Linear Feedback Shift Registers) with majority clocking. The total number of bits in these LFSRs is 19+22+23=64.
Every LFSR has it's own feedback loop, where a few "tapped bits" are xorred together to provide the next bit when the LFSR is shifted.
Every LFSR has one clock bit. Majority clocking means that only those LFSRs are clocked in which the clock bit is equal to the majority value of the 3 clock bits. That means that in every clock cycle at least two LFSRs are shifted. The probability that a register is shifted is 75% assuming randomly distributed clocking bits. Of the 8 possible combinations, only 2 make a particular register the minority.
Upon initialisation the state is zeroed out. Then the 64 bit secret key Kc (known to handset and bts) is loaded by xorring the bits to the rightmost bit of each LFSR before shifting them. The same is done for the 22 bit Frame Number, which is different for every burst, but publicly known. In these phases all LFSRs are clocked, so only after 22+64 clockings majority clocking kicks in.
Then the whole system is clocked forward 100 times (with majority clocking), and then two times 114 bits of keystream are recorded by xorring the leftmost bit of each LFSR.
Backclocking A5/1¶
Our current (jan 2010) tables and lookup code give us an A5/1 state which will generate the 64 bits of keystream we observe. By forward clocking the state and examining the keystream we can readily check if the internal state we found is indeed the internal state of the handset/bts.
We want to know the A5/1 state just after Kc is mixed in. By taking that as a starting point, and mixing in the Frame Number of a recorded burst, we can decode that burst.
We have to backclock the A5/1 state at least 100 times to get to the point where the Frame Number was mixed in, and then mix out the Frame Number to get to the desired result.
A single LFSR is easy to clock back. As in forward clocking the rightmost bit is determined by xorring the tapped bits together, in backward clocking the leftmost bit is determined by xorring the tapped bits, except the leftmost bit, with the rightmost bit.
Clocking back the entire A5/1 machine means that you have to account for majority clocking. This means that there are several states that could have lead up to the state observed. Since we need to know the state at least 100 clockings back, there normally is a multiplicity of such ancestor states which are equally probable to have been the actual state. Note that this implies that the 64 bit keystream space is therefore smaller than 264.
It is important to note that due to majority clocking not every combination of bits in the LFSRs form a valid state at this point. When looking at the clockbits of each LFSR, and the bit to the left of it, there are 26 combinations in total, of which 24 are impossible to clock back. 26 combinations can be clocked back in one way, 6 combinations in 2 ways, 6 combinations in 3 ways and 2 combinations in 4 ways. The expected number of ancestors is therefore (0*24+1*26+2*6+3*6+4*2)/64=1.
The dead ends thus introduced greatly reduce the number of ancestor states, and the expected value of the number of such ancestor states of randomly selected states in practice is 1.
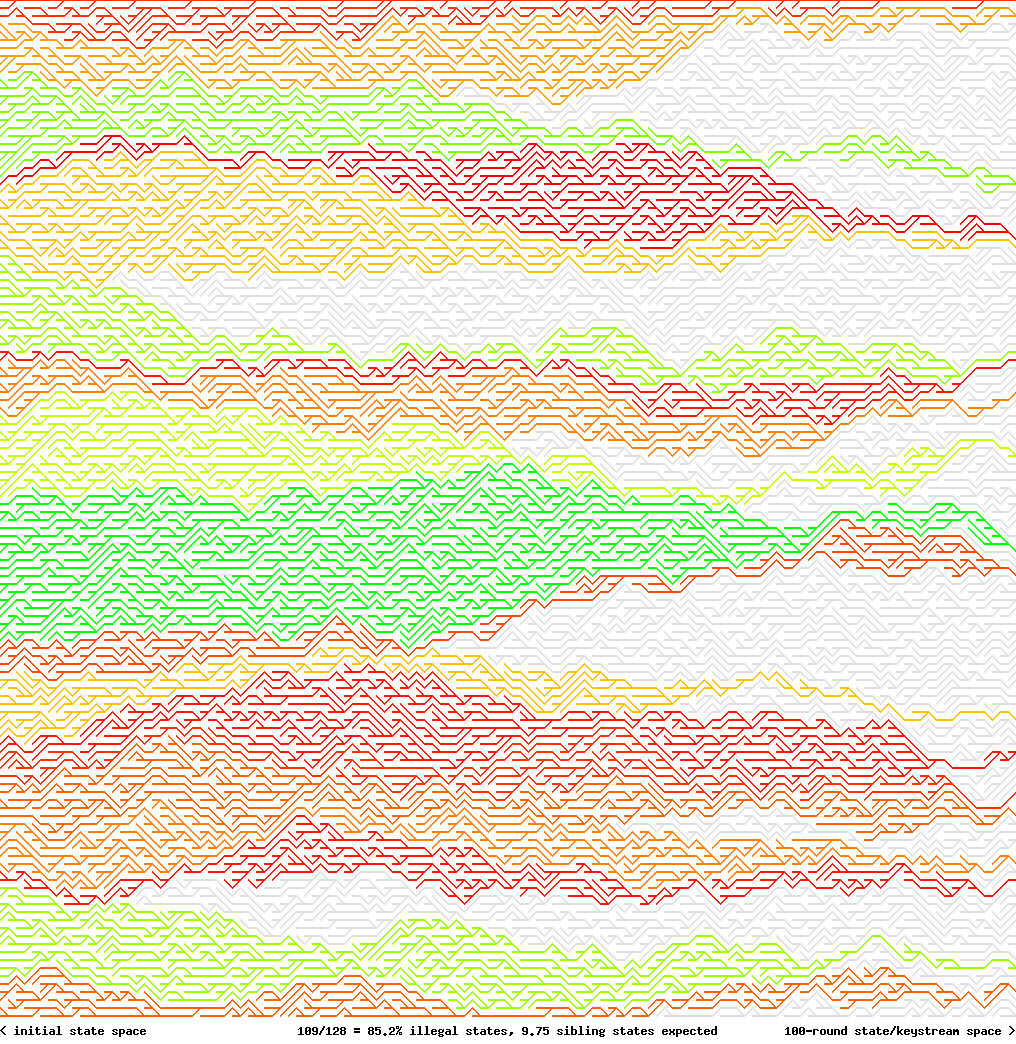
This figure shows what happens in state space. Grey paths are not accessible through forward clocking. Green paths have many ancestor states leading to the same keystream. Red paths have little ancestor states leading to the same keystream.
Even more states leading to the same keystream¶
Of course any state generated from state S through backclocking will eventually lead through state S again, and from that point on create the same keystream.
Another way to get states which generate the same keystream, is to clock forward N times, and clock back N times again, while checking if the correct keystream would be produced.
This way, any random state can be converted into 1.4 other states on average which generate the exact same keystream.
States which are the result of clocking forward 100 times (see optimizations, below) can be converted into 0.8 other states on average. However, if we also take into account that the resulting state must be clocked back 100 times, only 0.03 other valid states remain per state. This increases the initial state space leading up to an observed keystream by 3%.
These are the results of taking 100000 random samples and clocking forward/backward again. Note that the initial state is counted as well. (so 36934 states have no such siblings creating the same keystream)
| #siblstates | #F/B |
| 1 | 36934 |
| 2 | 12687 |
| 3 | 31251 |
| 4 | 14436 |
| 5 | 2865 |
| 6 | 997 |
| 7 | 674 |
| 8 | 65 |
| 9 | 43 |
| 10 | 37 |
| 12 | 5 |
| 13 | 3 |
| 15 | 2 |
| 20 | 1 |
| AVG: | 2.40 |
Optimizations under consideration¶
Currently in chain generation the produced 64 bits of keystream are used as the internal state for the next 64 bits of keystream generated. Finding a hit in the tables will then give a state which will in fact produce the 64 bits of keystream observed.
In practice, only 16% of randomly selected 64 bit states can be clocked back at least 100 times. The chance of finding a state/keystream in the tables, resulting in our target (the state just after Kc and the Frame Number are mixed in) is therefore greatly reduced. In some 5% of cases a valid state which will produce the same keystream can be found through forward/backward clocking an illegal state.
By taking the internal state after Kc and the Frame Number are mixed in, clocking that forward 100 times, and then taking 64 bits of keystream, we are sure that a state found in the tables is in fact valid. When we find a hit in the tables, all we need to do is clock forward 100 times to get at the state which will generate the observed keystream. Clocking back in practice then gives 13 ancestor states on average at the point where the frame number is mixed in.
The costs are that for every state-to-keystream calculation twice the CPU time is required. The benefits are that tables can be smaller and lookups will prove to have a higher success rate.
Updated by Sascha over 12 years ago · 4 revisions