KeystreamSpaceState and keystream space determined through backclocking random states¶

As discussed in Backclocking A5/1, not all A5/1 states can exist after 100 rounds of majority clocking.

Since the A5/1 state is 64 bits wide, the number of possible states is 264. Not every state can be clocked back. The following table gives the number of illegal states when considering backclocking.

16 back	57% illegal states
32 back	68% illegal states
48 back	74% illegal states
64 back	78% illegal states
80 back	82% illegal states
96 back	84% illegal states

This means that only 16% of states can actually exist after clocking forward 100 times.

This also implies that only 16% of possible 64 bit keystreams can exist. Since we take 64 bits of keystream as the next state in chain generation, we have to make sure that we map the reduced keystream space into the 264 size 64 bit space again, by using enough suitable round functions.

State and keystream space determined through forward and backclocking random states¶

When considering forward clocking a random state 100 times, and then clocking back, we generally arrive at between 1 and 100 states. The following chart shows the frequency of the number of sibling states when forward/backward clocking 100 times, based on evaluating one million random states. The number of ancestor states of a random state clocked back 100 times is shown as well (with the data point showing that 848000 of 1m states have no ancestors removed)

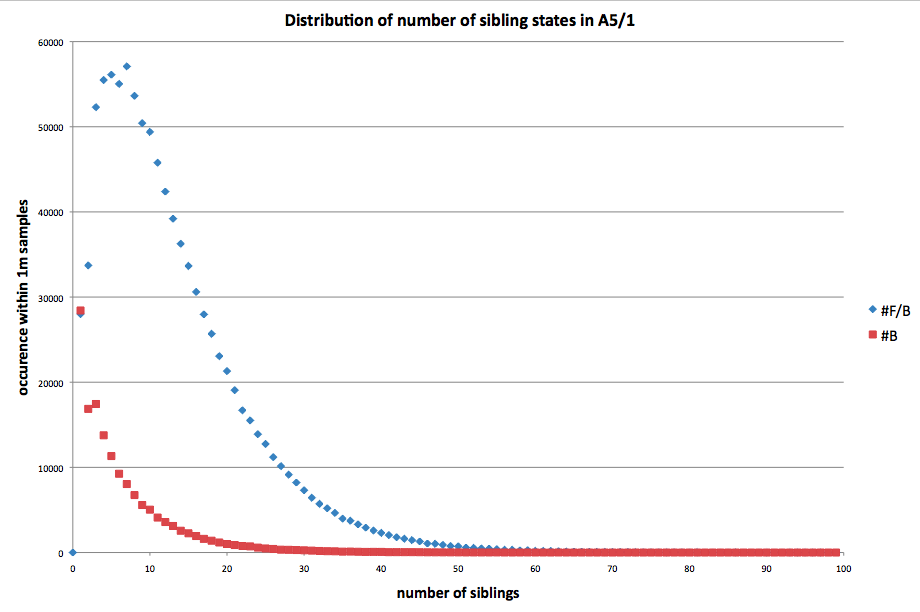
The weighed average for F/B clocking is 13.04, and for B clocking 1.00.

The peak is around 6. A uniform distribution from 264 sized initial state space to 16% of that space, would indeed lead one to expect that every valid state has 6 ancestors.

However, these numbers seem to indicate that A5/1 converges to a smaller group of favored states, since the weighed average is twice as high. In other words: we see 1m states that have 13m ancestors. This figure illustrates what happens:

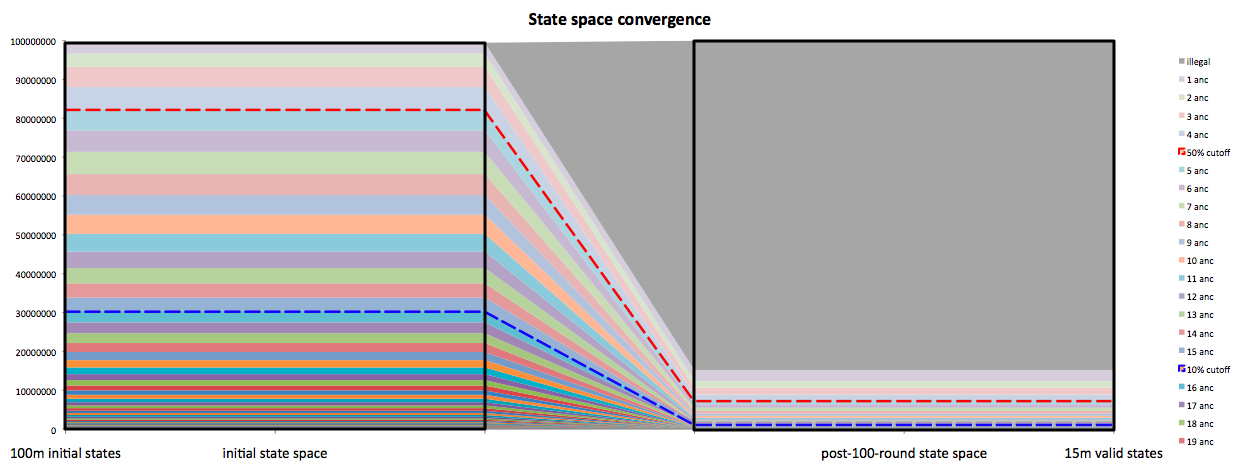
(based on clocking 100m random states F/B 100 times, as well as clocking 100m random states B 100 times, which gives perfectly matching data)

The two dashed lines show that:

half the actual keystreams find their origin in some 82% of initial states
    10% of actual keystreams find their origin in 30% of initial states

The figures below give more detailed data on group size distribution.

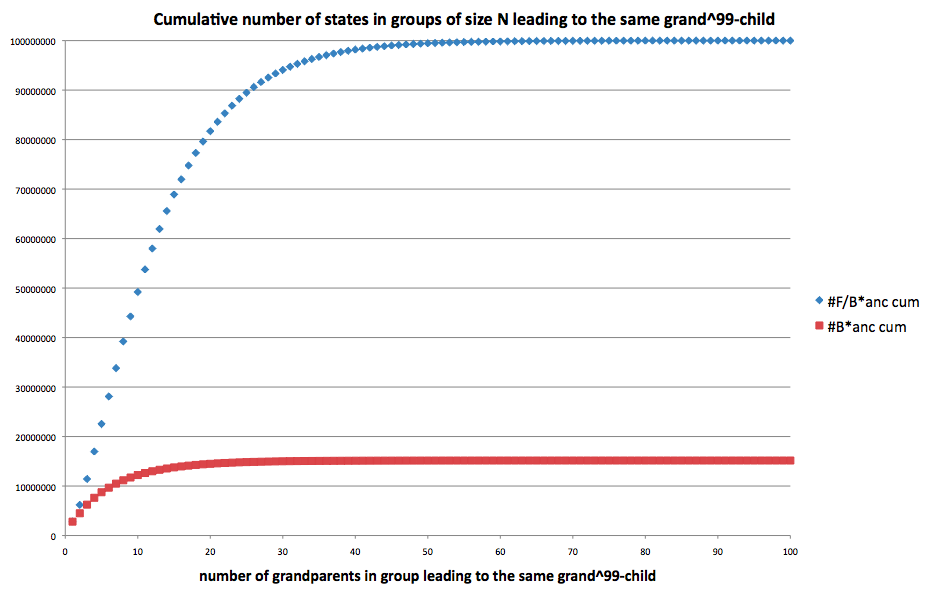
(Explanation: of all ancestors of 100m random states clocked forward 100 times, 20m out of 100m are in groups bigger than 19. There is a 20m/100m = 20% chance of hitting such a state.)

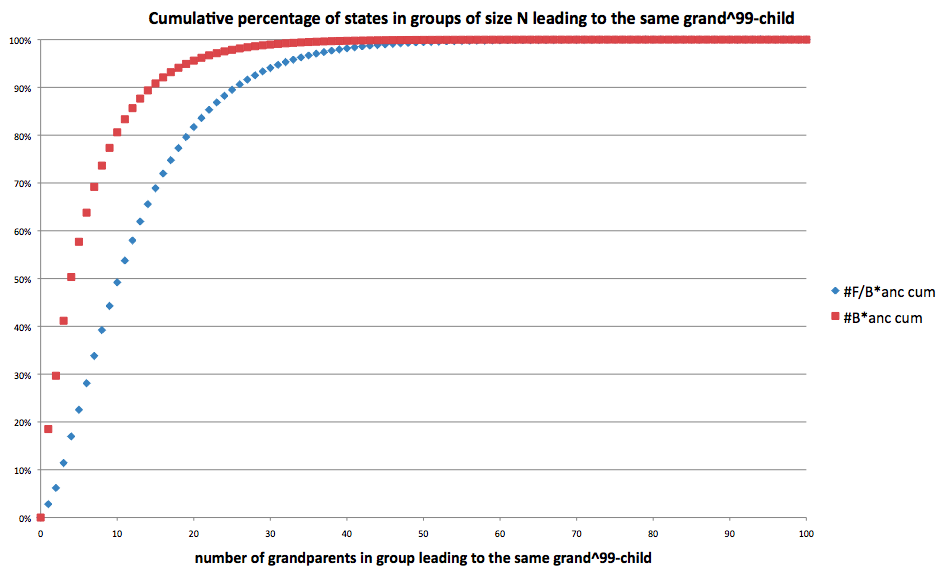
(Explanation: same as the above but in % of total.)

This figure clearly shows that (ceteris paribus) only using valid states will increase the amount of mergers.